
The association between an increase in entropy and a decrease in energy quality explains why all of the energy in fuels cannot be converted into mechanical energy. Therefore in general, since entropy naturally increases, energy quality will deteriorate. Seen in Figure 4, the energy quality decreases as entropy increases. Heat is a low-quality energy, whereas mechanical energy is a high-quality energy.

See the hyperphysics page on entropy for a more detailed discussion.Īssociated with entropy is the idea of "energy quality". This can be seen when shaking bricks in a can: the bricks are more likely to form a loose pile than to turn into a house. This is due to the fact that an open system can have its entropy decreased, as this ability to decrease the entropy is how refrigerators work! With that said, the Earth is an open system because of the solar energy to the Earth contributes to the Earth's energy flows.Įntropy is essentially a measure of "disorder", so the higher the entropy, the more disorder the system has. It is important to emphasize that this statement refers to a "closed system", meaning that there are no external influences on the system. Īnother statement, perhaps the most crucial in terms of understanding why the Clausius and Kelvin-Planck statements are true is about entropy (which can be thought of as disorder): " The entropy of a closed system can never decrease." For a more rigorous (but not as funny) write up of the refrigeration statement of the second law please see the hyperphysics Second Law:refrigerator page.įigure 4: With entropy decreasing as temperature increases, it can be shown that the a violation of this entropy statement would violate the Clausius statement of the Second Law. This statement is nicely captured in the humorous song 'The First and Second Laws of Thermodynamics' by Flanders and Swann. By analyzing how well a refrigerator can cool the cold reservoir, refrigerators carry with them a coefficient of performance. Due to this, a refrigerator is essentially a heat engine that runs in reverse. Therefore the net effect of the refrigerator is to make the cold reservoir colder by removing heat from it and moving that heat to the hot reservoir. In Figure 3, the refrigerator takes some heat from the cold reservoir, Q_c, does some work on it, W, and rejects some heat Q_H to the hot reservoir. The right part of the image in Figure 2 and 3 describe the impossible scenarios that the second law forbids, so a perfect refrigerator is analogous to a system's heat transfer operating at 100% efficiency. įigure 3: The Clausius statement of the Second Law of Thermodynamics forbids heat to flow from cold to hot unless external work is done. This is how refrigerators work to keep food inside of them cool, and why they can be felt blowing hot air out of their vents. Refrigerators work by transferring heat from the cold regions inside of the device to hot regions outside of it, thereby making the cold regions even cooler. This is how the refrigeration process works, and an example can be seen in Figure 1. The second law of thermodynamics claims that it is impossible for heat to spontaneously flow from a cold body to a hot body, but it can move in that way if some form of work is done. Everyday experience certainly supports this statement, but it is a deep physical concept limiting what's possible with energy. This is known as the Clausius statement, and explains why an ice cube will melt when placed in a bowl of hot water but ice will not form from water outside on a hot day. " Heat will always flow spontaneously from hotter substances to colder ones".

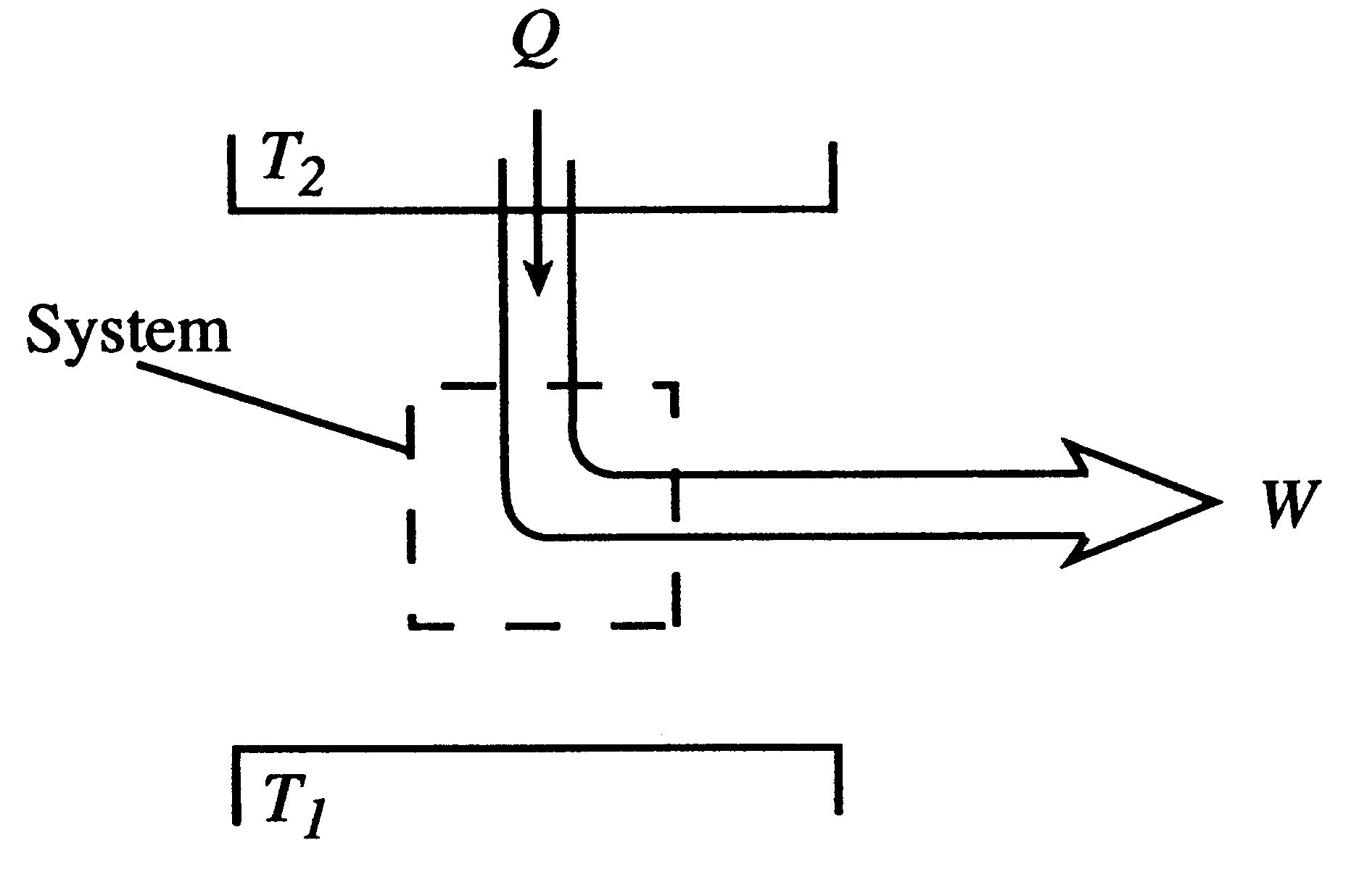
Although the Carnot efficiency can never be reached in reality, it is useful to compare to when looking at thermal efficiency of an engine.įor a more detailed study of this version of the second law please see the hyperphysics page on the second law: heat engines.Īlso known as the "Clausius statement", this is fundamental to how a refrigeration system works: Using an analysis of heat and work on an ideal engine, the maximum amount of work that can be achieved by a thermodynamic exchange between two specific temperatures is given by the Carnot efficiency. Waste heat is necessary for all engines, and the amount of work that is done by the input of heat gives the thermal efficiency of a system. This statement is important to understand in terms of practicality of heat engines. Figure 2: It is impossible for the thermal efficiency of an engine to be 100%, where all of the heat from the hot body would be transferred to useful work.


 0 kommentar(er)
0 kommentar(er)
